A (Long) Peek into Reinforcement Learning: Part1

[A (Long) Peek into Reinforcement Learning

Lil’Log](https://lilianweng.github.io/posts/2018-02-19-rl-overview/)

Key Concepts

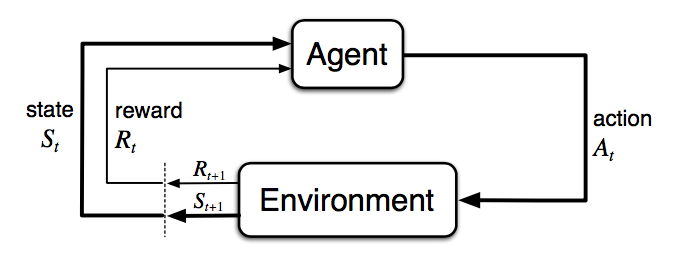
The agent can stay in one of many states ($s\in \mathcal{S}$) of the environment, and choose to take one of many actions ($a\in \mathcal{A}$) to switch from one state to another. Which state the agent will arrive in is decided by transition probabilities between states ($P$). Once an action is taken, the environment delivers a reward ($r\in \mathcal{R}$) as feedback.

• Model-based: model is known
• Model-free: No dependency on model
• On-policy: train on deterministic outcomes or samples
• Off-policy: train on transitions or episodes of different behavior policy

State-transition Function: \[\begin{align} P_{ss'}^a & = P(s', s, a) \\ & = \mathbb{P}[S_{t+1} = s', S_t = s, A_t = a] \\ & = \sum_{r \in \mathcal{R}} P(s', r|s, a) \end{align}\]

Reward function $R$ \[\begin{align} R(s, a) &= \mathbb{E}[R_{t+1}|S_t = s, A_t = a] \\ &= \sum_{r \in \mathcal{R}} r \sum_{s' \in S} P(s', r|s, a) \end{align}\]

Policy:

• Deterministic: $\pi(s)=a$
• Stochastic: $\pi(a\mid s)= \mathbb{P}_\pi[A=a\mid S=s]$

Return: \[G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t+k+1}\]

The state-value of a state $s$ is the expected return: \[V_\pi(s)=\mathbb{E}_\pi[G_t\mid S_t=s]\]

Action-value: \[Q_\pi(s,a) = \mathbb{E}_\pi[G_t\mid S_t=s, A_t = a]\]

We can use probability distribution + Q-values -> State Value: \[V_\pi(s) = \sum_{a\in \mathbb{A}} Q_\pi(s,a) \pi(a\mid s)\]

Action Advantage Function: \[A_\pi(s,a) = Q_\pi(s,a)-V_\pi(s)\]

Thus, we get the optimal policy: \[\begin{cases} V_*(s)=\underset{\pi}{\max} V_\pi(s) \\ \pi_* = \arg \underset{\pi}{\max} V_\pi(s) \\ V_{\pi_*} = V_* \end{cases}\]

Same as $Q$

Markov Decision Processes

In Markov Decision Processes, future only depends on the current state.

Eg for MDP

Bellman Equations

Current $V$ is future $R$ + future $V$ \[\begin{aligned} V(s) & =\mathbb{E}\left[G_t \mid S_t=s\right] \\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\ldots \mid S_t=s\right] \\ & =\mathbb{E}\left[R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) \mid S_t=s\right] \\ & =\mathbb{E}\left[R_{t+1}+\gamma G_{t+1} \mid S_t=s\right] \\ & =\mathbb{E}\left[R_{t+1}+\gamma V\left(S_{t+1}\right) \mid S_t=s\right] \end{aligned}\]

Similarly for $Q$ value \[\begin{aligned} Q(s, a) & =\mathbb{E}\left[R_{t+1}+\gamma V\left(S_{t+1}\right) \mid S_t=s, A_t=a\right] \\ & =\mathbb{E}\left[R_{t+1}+\gamma \mathbb{E}_{a \sim \pi} Q\left(S_{t+1}, a\right) \mid S_t=s, A_t=a\right] \end{aligned}\]

Bellman Expectation Equations

Recursive update process \[\begin{aligned} {\color[rgb]{0.29,0.56,0.89}V_\pi(s)} & = \sum_{a \in \mathcal{A}} \pi(a \mid s) {\color{green}Q_\pi(s, a)} &(1)\\ {\color{green}Q_\pi(s, a)} & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a {\color[rgb]{0.29,0.56,0.89}V_\pi\left(s^{\prime}\right)} &(2)\\ V_\pi(s) & =\sum_{a \in \mathcal{A}} \pi(a \mid s)\left(R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a V_\pi\left(s^{\prime}\right)\right) &{\color{green}(2)Q_\pi \rightarrow (1)}\\ Q_\pi(s, a) & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a \sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} \mid s^{\prime}\right) Q_\pi\left(s^{\prime}, a^{\prime}\right) &{\color[rgb]{0.29,0.56,0.89}(1)V_\pi \rightarrow(2)} \end{aligned}\]

Bellman Optimality Equations: The Optimal Value $V_, Q_$ are best return. \[\begin{aligned} {\color[rgb]{0.29,0.56,0.89}V_*(s)} & =\max _{a \in \mathcal{A}} {\color{green}Q_*(s, a) } \\ {\color{green}Q_*(s, a)} & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a {\color[rgb]{0.29,0.56,0.89}V_*\left(s^{\prime}\right)} \\ V_*(s) & =\max _{a \in \mathcal{A}}\left(R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a V_*\left(s^{\prime}\right)\right) &{\color{green}(2)Q_\pi \rightarrow (1)}\\ Q_*(s, a) & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a \max _{a^{\prime} \in \mathcal{A}} Q_*\left(s^{\prime}, a^{\prime}\right) &{\color[rgb]{0.29,0.56,0.89}(1)V_\pi \rightarrow(2)} \end{aligned}\]

However, in most scenarios, we do not know $P^a_{ss^\prime}$, or $R(s,a)$, so we can not directly use Bellmen equations to solve this problem.